Understanding Radical Expressions In Algebra
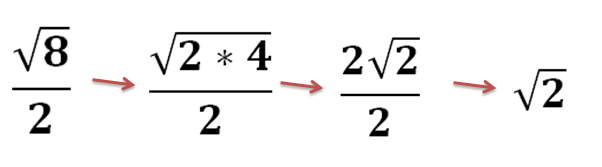
Understanding Radical Expressions In Algebra. Discover more detailed and exciting information on our website. Click the link below to start your adventure: Visit Best Website. Don't miss out!
Table of Contents
Decoding the Mystery: A Comprehensive Guide to Understanding Radical Expressions in Algebra
Algebra can often feel like navigating a dense forest, but with the right tools and understanding, even the trickiest concepts become manageable. One such concept that often stumps students is the world of radical expressions. This comprehensive guide will illuminate the intricacies of radical expressions, equipping you with the knowledge to confidently tackle them. Whether you're a high school student grappling with algebra or an adult learner brushing up on your math skills, this article will help you master this crucial element of algebra.
What are Radical Expressions?
At its core, a radical expression is any mathematical expression containing a radical symbol, often denoted as √ (square root), but also encompassing cube roots (∛), fourth roots (∜), and so on. These symbols represent the inverse operation of exponentiation. For example, √9 = 3 because 3² = 9. The number under the radical symbol is called the radicand.
-
Key Components: Understanding the parts of a radical expression is crucial. This includes the radicand (the number or expression inside the radical), the index (the small number indicating the type of root—2 for square root, 3 for cube root, etc.), and the radical symbol itself.
-
Examples of Radical Expressions:
- √16 (square root of 16)
- ∛27 (cube root of 27)
- √(x² + 4) (square root of a binomial expression)
- ∜16x⁴ (fourth root of a polynomial)
Simplifying Radical Expressions: Essential Techniques
Simplifying radical expressions is a fundamental skill. Here are some key strategies:
-
Prime Factorization: Breaking down the radicand into its prime factors is often the first step. This allows you to identify perfect squares, cubes, or other perfect powers that can be simplified. For instance, √12 can be simplified to √(2² * 3) = 2√3.
-
Rules of Exponents: Understanding exponent rules is crucial for simplifying radicals. Remember that √a * √b = √(ab) and √a / √b = √(a/b) (assuming a and b are non-negative).
-
Rationalizing the Denominator: This technique involves eliminating radicals from the denominator of a fraction. For example, to rationalize 1/√2, you multiply both the numerator and denominator by √2, resulting in √2/2.
Solving Equations with Radical Expressions
Equations containing radical expressions require specific techniques to solve. These often involve:
-
Isolating the Radical: The first step is usually to isolate the radical term on one side of the equation.
-
Squaring (or Cubing, etc.): To eliminate the radical, you raise both sides of the equation to the power of the index (e.g., squaring for square roots, cubing for cube roots). Important Note: Remember to check your solutions, as squaring both sides can introduce extraneous solutions.
-
Solving the Resulting Equation: After eliminating the radical, you solve the resulting equation using standard algebraic techniques.
Mastering Radical Expressions: Practice Makes Perfect
The key to mastering radical expressions lies in consistent practice. Work through various examples, focusing on simplifying expressions and solving equations. Online resources, textbooks, and practice worksheets are excellent tools to hone your skills.
Conclusion: Unlocking the Power of Radical Expressions
Understanding radical expressions is vital for success in algebra and beyond. By mastering the techniques outlined in this article and dedicating time to practice, you can confidently navigate the world of radicals and unlock a deeper understanding of algebraic concepts. Start practicing today and witness your algebra skills soar!
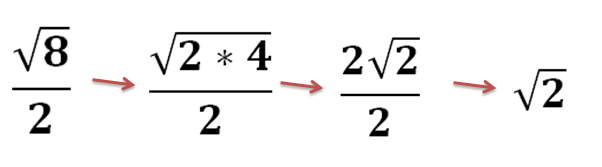
Thank you for visiting our website wich cover about Understanding Radical Expressions In Algebra. We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and dont miss to bookmark.
Featured Posts
-
 Temoignages Apres Les Tirs D Agents De La Surete En Gare
Feb 05, 2025
Temoignages Apres Les Tirs D Agents De La Surete En Gare
Feb 05, 2025 -
 Daufuskie Island Beyond The Beaches A Cultural Journey
Feb 05, 2025
Daufuskie Island Beyond The Beaches A Cultural Journey
Feb 05, 2025 -
 Contradictory Medical Testimony Emerges In Lucy Letby Trial
Feb 05, 2025
Contradictory Medical Testimony Emerges In Lucy Letby Trial
Feb 05, 2025 -
 Gare Sous Tension Enquete Sur Les Tirs Impliquant La Surete Ferroviaire
Feb 05, 2025
Gare Sous Tension Enquete Sur Les Tirs Impliquant La Surete Ferroviaire
Feb 05, 2025 -
 Convert 26 Celsius To Fahrenheit Simple Calculation And Explanation
Feb 05, 2025
Convert 26 Celsius To Fahrenheit Simple Calculation And Explanation
Feb 05, 2025
Latest Posts
-
 Used Cars In Fargo Craigslist Listings And Pricing
Feb 05, 2025
Used Cars In Fargo Craigslist Listings And Pricing
Feb 05, 2025 -
 Successions Shiv Roy Analyzing Her Moral Compass And Choices
Feb 05, 2025
Successions Shiv Roy Analyzing Her Moral Compass And Choices
Feb 05, 2025 -
 Understanding Turmeric And Dogs Health Benefits Risks And Safe Use
Feb 05, 2025
Understanding Turmeric And Dogs Health Benefits Risks And Safe Use
Feb 05, 2025 -
 What Time Is It In Boston Right Now A Quick Guide To Boston Time
Feb 05, 2025
What Time Is It In Boston Right Now A Quick Guide To Boston Time
Feb 05, 2025 -
 Court Appearance For Man Charged In Fentanyl Death Case
Feb 05, 2025
Court Appearance For Man Charged In Fentanyl Death Case
Feb 05, 2025
