Simplifying Radical Expressions: Common Mistakes To Avoid
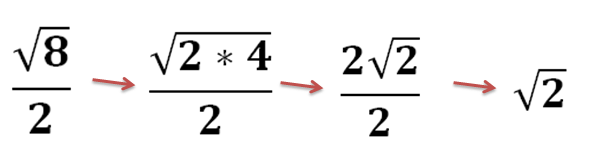
Discover more detailed and exciting information on our website. Click the link below to start your adventure: Visit Best Website. Don't miss out!
Table of Contents
Simplifying Radical Expressions: Common Mistakes to Avoid
Are you struggling with simplifying radical expressions? Do square roots, cube roots, and beyond leave you feeling frustrated? You're not alone! Many students find simplifying radicals challenging, often making the same common mistakes. This article will highlight those pitfalls and provide you with the strategies to conquer radical simplification. Mastering this skill is crucial for success in algebra, precalculus, and beyond. Let's dive into the common errors and learn how to avoid them.
H2: Understanding the Basics of Radical Simplification
Before tackling common mistakes, let's ensure we're on the same page regarding the fundamentals of simplifying radical expressions. The process involves finding the perfect square factors (or perfect cube factors, etc.) within the radicand (the number inside the radical symbol). For example, simplifying √12 involves finding the largest perfect square that divides 12, which is 4. We can then rewrite √12 as √(4 x 3) = √4 x √3 = 2√3.
H2: Common Mistakes When Simplifying Radical Expressions
Students frequently encounter several common issues when simplifying radical expressions. Let's examine them closely:
H3: Mistake 1: Incorrectly Identifying Perfect Squares/Cubes
One of the most frequent mistakes is failing to identify the largest perfect square (or cube, etc.) factor within the radicand. For instance, consider simplifying √48. While you might identify 4 as a perfect square factor (√48 = √(4 x 12) = 2√12), this isn't fully simplified. The correct approach involves recognizing that 16 is also a factor of 48 (48 = 16 x 3), leading to the simplified form 4√3.
- Tip: Create a list of perfect squares (1, 4, 9, 16, 25, 36, etc.) and perfect cubes (1, 8, 27, 64, etc.) to quickly identify factors.
H3: Mistake 2: Incorrect Simplification of Coefficients
Errors often occur when dealing with coefficients outside the radical symbol. For example, simplifying 3√20 often leads to incorrect answers. The correct approach: 3√20 = 3√(4 x 5) = 3(2√5) = 6√5. Failing to multiply the coefficient (3) by the simplified radical coefficient (2) is a common oversight.
H3: Mistake 3: Improper Handling of Variables
Simplifying radicals containing variables requires a different approach. Remember that √x² = |x| (the absolute value of x). This is crucial because x could be negative. For example, simplifying √(9x⁴) requires considering the absolute value: √(9x⁴) = |3x²|. Ignoring the absolute value leads to an incomplete or incorrect answer.
- Tip: Always remember to consider the absolute value when dealing with even roots of variables.
H3: Mistake 4: Adding or Subtracting Radicals Incorrectly
You can only add or subtract radicals if they have the same radicand and index. For example, 2√5 + 3√5 = 5√5. However, you cannot directly simplify 2√5 + 3√2. First, simplify each radical if possible, then add or subtract only those with matching radicands and indices.
H2: Practice Makes Perfect
The key to mastering radical simplification is practice. Work through numerous examples, focusing on identifying the largest perfect square (or cube) factors, handling coefficients correctly, and properly simplifying expressions with variables.
H2: Resources for Further Learning
Need extra help? There are many online resources available. Search for "simplifying radical expressions practice problems" or explore educational websites and videos for further guidance.
By understanding these common mistakes and implementing the tips provided, you can significantly improve your skills in simplifying radical expressions. Now go forth and conquer those radicals!
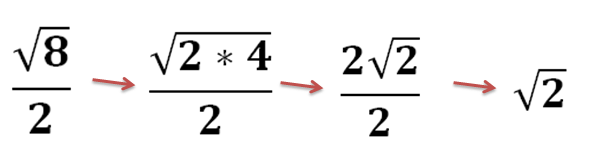
Thank you for visiting our website wich cover about Simplifying Radical Expressions: Common Mistakes To Avoid. We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and dont miss to bookmark.
Featured Posts
-
 Exploring The Versatility Of Linda Hunts Acting Career
Feb 05, 2025
Exploring The Versatility Of Linda Hunts Acting Career
Feb 05, 2025 -
 Fantastic Four Trailer Uncovering The Galactus Mystery And More
Feb 05, 2025
Fantastic Four Trailer Uncovering The Galactus Mystery And More
Feb 05, 2025 -
 Stuffersb Unveiling The Mysteries
Feb 05, 2025
Stuffersb Unveiling The Mysteries
Feb 05, 2025 -
 Venom Let There Be Carnage Comparing The Film To The Comic Book Source Material
Feb 05, 2025
Venom Let There Be Carnage Comparing The Film To The Comic Book Source Material
Feb 05, 2025 -
 Met Police Officer Faces Scrutiny In Sam Kerr Trial
Feb 05, 2025
Met Police Officer Faces Scrutiny In Sam Kerr Trial
Feb 05, 2025
Latest Posts
-
 Dive Into The Bloodlines New Final Destination Teaser Trailer Breakdown
Feb 05, 2025
Dive Into The Bloodlines New Final Destination Teaser Trailer Breakdown
Feb 05, 2025 -
 Dodgers Vs Yankees Head To Head Player Stats Showdown
Feb 05, 2025
Dodgers Vs Yankees Head To Head Player Stats Showdown
Feb 05, 2025 -
 C8 Corvette Mid Cycle Refresh Release Date Speculation
Feb 05, 2025
C8 Corvette Mid Cycle Refresh Release Date Speculation
Feb 05, 2025 -
 Seine Saint Denis Mystere Autour De La Mort D Un Homme De 27 Ans
Feb 05, 2025
Seine Saint Denis Mystere Autour De La Mort D Un Homme De 27 Ans
Feb 05, 2025 -
 Previsions Meteo Chutes De Neige Importantes Mardi Dans Les Hauts De France
Feb 05, 2025
Previsions Meteo Chutes De Neige Importantes Mardi Dans Les Hauts De France
Feb 05, 2025
